REVOLUTIONARY GEOMETRY: A Foundation for Nature-Based Architecture
by JAMES JACOBS
July 2003
page 1 | 2
Historically, simple geometric forms have been the basis for envisioning structure in architecture. It follows that a study of advanced geometric forms may provide the basis for envisioning advanced structures in architecture.
There is no historical record of new geometric structural systems being revealed since the discovery of the circle, square and triangle. The geometric structural system of the fourth archetypal form, the spiral—in its 3-D form, the the helix—has been uncovered and developed over the past 25 years by the author.
Helical Geometry is the study of geometry within the tetrahedron, the most fundamental of the 5 Platonic Solids of Solid Geometry.
 |
 |
|
| Fig. 1 The tetrahedron, the most basic of the 5 Platonic Solids | Fig. 2 The Helical Field Geometry within the tetrahedron |
Helical Geometry is the geometry of the straight twisted rod (Fig. 3), in the same way that Plane and Solid Geometry are the geometries of the straight rod. (Fig. 4) These are two distinctly different representations of distance, and so, two distinctly different approaches to understanding the geometric properties of space.
| Fig. 3 The straight twisted rod of
Helical Geometry |
| Fig. 4 The straight rod of Plane and Solid Geometry |
|
|
The geometric forms of Plane and Solid Geometry continue to be the basis for the way we design and build, as well as for the way we think about the laws of nature and how nature builds. The new geometrical system of Helical Geometry, by redefining distance in space as having a simultaneous measurable degrees-of-rotation, or twist, has profound implications for the foundations of our existing knowledge.
Literally, Helical Geometry adds new meaning to our ideas of what is "rational." It is not too bold to suggest that Helical Geometry offers a foundation for advancement in all areas of knowledge as it changes the way we think about that most fundamental concept, distance in space. This article discusses Helical Geometry, its correspondence with Nature, and its incorporation of existing geometric knowledge.
Geometry's Correspondence with Nature
Geometry is an attempt to understand the source of the symmetry seen in nature, and the structural order of that symmetry in space. The search for this understanding can be approached in two ways, numerically (i.e. mathematically), or structurally. Modern science uses the mathematical modeling approach, assuming that numerical models or formulas will reveal the source of symmetry in space. The ancient Greek geometers used the structural modeling approach, assuming that structural models would reveal the source of symmetry in nature, and, express a numerical model, the formula of a mathematical theorem.
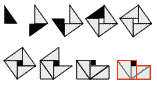
The geometer Pythagoras was credited with first showing a correspondence between a geometric structure and the source of symmetry in space around 350 BC. He demonstrated that two of the properties of the source of symmetry in Nature are the right angle and four-fold rotation. The archetypal geometric form he used was the triangle containing a ninety-degree angle, a plane right-angled triangle. He showed how this family of geometric structures reveals a correspondence with nature's symmetry in 2-dimensional space.
 |
|
|
Fig. 5 The plane right-angled triangle's proof of correspondence with the 4-fold, 2-dimensional symmetry in Nature.
|
Pythagoras rotated this unique type of triangle (with its one right angle) in a fourfold pattern, its longest side facing outward, and so generated the symmetrical boundaries of a perfect square. Then, by a redistribution of the triangles making up the symmetrical pattern, he showed that the remaining two sides of the right-angled triangle structure also generated the symmetry of two perfect squares. And, that these two squares of symmetry are contained within and equivalent to the symmetry of the square of the longest side. (Fig. 5) This is true of all triangles having a right-angle, and not true of any other archetypal geometric structure. (Ref: "The Ascent of Man", Jacob Bronowski)
This unique type of 2-dimensional geometrical structure having a right-angle visibly demonstrated its correspondence with nature's symmetry in 2-dimensional space. For this reason, the single unique property of this geometrical structure, its right-angle, and, the fourfold rotation required to generate the symmetry of the square, are considered to be properties of the source of the symmetry in 2-dimensional space.
All plane right-angled triangles express a numerical model, the formula of the mathematical theorem which states: The square of the longest side of the plane right-angled triangle is equal to the sum of the squares of the two shortest sides, which is, c2=a2+b2, the formula of the Pythagorean Theorem, the most important theorem in all mathematics. The plane right-angled triangle expresses the Table of Natural Trigonometric Functions of Sines and Cosines, without which there would be neither Newtons's laws of nature, nor Einstein's Theories of Relativity. The validity of science's natural laws and universal theories, dependent as they are on the plane right-angled triangle, speaks for the correspondence of this geometrical structure with Nature's symmetry, and the source of symmetry in 2-dimensional space. If there were no such correspondence, then its numerical expressions of the plane right-angled triangle would not have led to subsequent mathematical descriptions corresponding with the laws of nature and universe.
Helical Geometry uses a structural modeling approach similar to that of the ancient Greek geometer's approach to understand the source of symmetry in nature. It demonstrates its correspondence with the 3-dimensional symmetry in space by the fourfold rotation of a unique geometrical structure, the helical building panel, that mimics the 3-dimensional symmetry of the natural form of a molecule-thin liquid membrane, the soap-film (Fig. 6). In addition, Helical Geometry's unique geometrical structure shows a direct correspondence with the geometry of the plane right-angled triangle, and expresses the Table of Natural Trigonometric Functions of Sines and Cosines, but in 3-dimensional space as opposed to 2-dimensional space.
 |
 |
 |
 |
| Fig. 6 The helical building panel's proof (#1 of 2) of correspondence with the 4-fold, 3-dimensional symmetry in Nature. | |||